https://doi.org/10.1140/epjc/s10052-021-09401-4
Regular Article - Theoretical Physics
Manifest form of the spin-local higher-spin vertex 
1
Lebedev Physical Institute, Leninsky Prospect 53, 119991, Moscow, Russia
2
Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Science”, Nakhimovsky Prospect 36-1, 117218, Moscow, Russia
Received:
20
June
2021
Accepted:
24
June
2021
Published online:
13
July
2021
Vasiliev generating system of higher-spin equations allowing to reconstruct nonlinear vertices of field equations for higher-spin gauge fields contains a free complex parameter 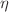 . Solving the generating system order by order one obtains physical vertices proportional to various powers of
. Solving the generating system order by order one obtains physical vertices proportional to various powers of 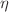 and
and  . Recently
. Recently 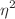 and
and 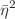 vertices in the zero-form sector were presented in Didenko et al. (JHEP 2012:184, 2020) in the Z-dominated form implying their spin-locality by virtue of Z-dominance Lemma of Gelfond and Vasiliev (Phys. Lett. B 786:180, 2018). However the vertex of Didenko et al. (2020) had the form of a sum of spin-local terms dependent on the auxiliary spinor variable Z in the theory modulo so-called Z-dominated terms, providing a sort of existence theorem rather than explicit form of the vertex. The aim of this paper is to elaborate an approach allowing to systematically account for the effect of Z-dominated terms on the final Z-independent form of the vertex needed for any practical analysis. Namely, in this paper we obtain explicit Z-independent spin-local form for the vertex
vertices in the zero-form sector were presented in Didenko et al. (JHEP 2012:184, 2020) in the Z-dominated form implying their spin-locality by virtue of Z-dominance Lemma of Gelfond and Vasiliev (Phys. Lett. B 786:180, 2018). However the vertex of Didenko et al. (2020) had the form of a sum of spin-local terms dependent on the auxiliary spinor variable Z in the theory modulo so-called Z-dominated terms, providing a sort of existence theorem rather than explicit form of the vertex. The aim of this paper is to elaborate an approach allowing to systematically account for the effect of Z-dominated terms on the final Z-independent form of the vertex needed for any practical analysis. Namely, in this paper we obtain explicit Z-independent spin-local form for the vertex  for its
for its 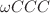 -ordered part where
-ordered part where 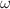 and C denote gauge one-form and field strength zero-form higher-spin fields valued in an arbitrary associative algebra in which case the order of product factors in the vertex matters. The developed formalism is based on the Generalized Triangle identity derived in the paper and is applicable to all other orderings of the fields in the vertex.
and C denote gauge one-form and field strength zero-form higher-spin fields valued in an arbitrary associative algebra in which case the order of product factors in the vertex matters. The developed formalism is based on the Generalized Triangle identity derived in the paper and is applicable to all other orderings of the fields in the vertex.
© The Author(s) 2021
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3




