https://doi.org/10.1140/epjc/s10052-021-09182-w
Regular Article - Theoretical Physics
A massless scalar particle coupled to the Wahlquist metric
1
Department of Physics, Istanbul Technical University, Istanbul, Turkey
2
Department of Physics, Mimar Sinan Fine Arts University, Istanbul, Turkey
Received:
3
February
2021
Accepted:
23
April
2021
Published online:
5
May
2021
We study the solutions of the wave equation where a massless scalar field is coupled to the Wahlquist metric, a type-D solution. We first take the full metric, and then write simplifications of the metric by taking some of the constants in the metric null. When we do not equate any of the arbitrary constants in the metric to zero, we find the solution is given in terms of the general Heun function, apart from some simple functions multiplying this solution. This is also true, if we equate one of the constants 
or 
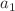to zero. When both the NUT related constant 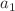and are zero, the singly confluent Heun function is the solution. When we also equate the constant 
to zero, we get the double confluent Heun-type solution. In the latter two cases, we have an exponential and two monomials raised to powers multiplying the Heun type function. Thus, we generalize the Batic et al. result for type-D metrics for this metric and show that all variations of the Wahlquist metric give Heun type solutions.
© The Author(s) 2021
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
