https://doi.org/10.1140/epjc/s10052-021-08888-1
Regular Article – Theoretical Physics
Lyapunov exponent, ISCO and Kolmogorov–Senai entropy for Kerr–Kiselev black hole
1
Department of Mathematics, Jadavpur University, 700032, Kolkata, West Bengal, India
2
Department of Physics, National Defence Academy, 411023, Khadakwasla, Pune, India
Received:
16
July
2020
Accepted:
16
January
2021
Published online:
26
January
2021
Geodesic motion has significant characteristics of space-time. We calculate the principle Lyapunov exponent (LE), which is the inverse of the instability timescale associated with this geodesics and Kolmogorov–Senai (KS) entropy for our rotating Kerr–Kiselev (KK) black hole. We have investigate the existence of stable/unstable equatorial circular orbits via LE and KS entropy for time-like and null circular geodesics. We have shown that both LE and KS entropy can be written in terms of the radial equation of innermost stable circular orbit (ISCO) for time-like circular orbit. Also, we computed the equation marginally bound circular orbit, which gives the radius (smallest real root) of marginally bound circular orbit (MBCO). We found that the null circular geodesics has larger angular frequency than time-like circular geodesics (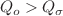
). Thus, null-circular geodesics provides the fastest way to circulate KK black holes. Further, it is also to be noted that null circular geodesics has shortest orbital period 
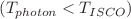among the all possible circular geodesics. Even null circular geodesics traverses fastest than any stable time-like circular geodesics other than the ISCO.
© The Author(s) 2021
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
