https://doi.org/10.1140/epjc/s10052-020-7877-y
Regular Article - Theoretical Physics
Stochastic inflaton wave equation from an expanding environment
Institute of Theoretical Physics, University of Wroclaw, 50-204, Wrocław, Poland
* e-mail: zbigniew.haba@uwr.edu.pl
Received:
20
January
2020
Accepted:
24
March
2020
Published online:
13
April
2020
We discuss the inflaton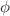 
in an environment of scalar fields 
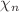on flat and curved manifolds. We average over the environmental fields 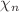. We study a contribution of superhorizon 
as well as subhorizon 
modes 
. As a result we obtain a stochastic wave equation with a friction and noise. We show that in the subhorizon regime in field theory a finite number of fields is sufficient to produce a friction and diffusion owing to the infinite number of degrees of freedom corresponding to different 
in . We investigate the slow roll and the Markovian approximations to the stochastic wave equation. A determination of the metric from the stochastic Einstein–Klein–Gordon equations is briefly discussed.
© The Author(s), 2020
