https://doi.org/10.1140/epjc/s10052-019-6992-0
Regular Article - Theoretical Physics
Multipole analysis for linearized 
gravity with irreducible Cartesian tensors
Institute of High Energy Physics and Theoretical Physics Center for Science Facilities, Chinese Academy of Sciences, Beijing, 100049, People’s Republic of China
* e-mail: bofengw@pku.edu.cn
Received:
6
May
2019
Accepted:
24
May
2019
Published online:
17
June
2019
The field equations of gravity are rewritten in the form of obvious wave equations with the stress–energy pseudotensor of the matter fields and the gravitational field as its source under the de Donder condition. The linearized field equations of gravity are the same as those of linearized f(R) gravity, and thus, their multipole expansions under the de Donder condition are also the same. It is also shown that the Gauss–Bonnet curvature scalar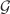 
does not contribute to the effective stress–energy tensor of gravitational waves in linearized gravity, though 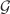plays an important role in the nonlinear effects in general. Further, by applying the 1 / r expansion in the distance to the source to the linearized gravity, the energy, momentum, and angular momentum carried by gravitational waves in linearized gravity are provided, which shows that 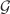, unlike the nonlinear term 
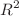in the gravitational Lagrangian, does not contribute to them either.
© The Author(s), 2019
