https://doi.org/10.1140/epjc/s10052-019-6899-9
Regular Article - Theoretical Physics
A generalized Finch–Skea class one static solution
1
Department of Physics, National Defence Academy, Khadakwasla, Pune, 411023, India
2
Department of Mathematical and Physical Sciences, College of Arts and Science, University of Nizwa, Nizwa, Sultanate of Oman
3
Department of Mathematics, Jadavpur University, Kolkata, West Bengal, 700032, India
4
Departamento de Física, Facultad de ciencias básicas, Universidad de Antofagasta, Casilla 170, Antofagasta, Chile
* e-mail: sunil@unizwa.edu.om
Received:
10
April
2019
Accepted:
19
April
2019
Published online:
3
May
2019
In the present article, we discuss relativistic anisotropic solutions of Einstein field equations for the spherically symmetric line element under the class I condition. To do so we apply the embedding class one technique using Eisland condition. Within this approach, one arrives at a particular differential equation that links the two metric components 
and 
. In order to obtain the full space–time description inside the stellar configuration we ansatz the generalized form of metric component 
corresponding to the Finch–Skea solution. Once the space–time geometry is specified we obtain the complete thermodynamic description i.e. the matter density 
, the radial, and tangential pressures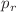 
and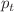 
, respectively. Graphical analysis shows that the obtained model respects the physical and mathematical requirements that all ultra-high dense collapsed structures must obey. The M–R diagram suggests that the solution yields stiffer EoS as parameter n increases. The M–I graph is in agreement with the concepts of Bejgar et al. (Mon Not R Astron Soc 364:635, 2005) that the mass at 
is lesser by few percent (for this solution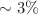 
) from 
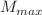. This suggests that the EoSs is without any strong high-density softening due to hyperonization or phase transition to an exotic state.
© The Author(s), 2019
