https://doi.org/10.1140/epjc/s10052-018-6099-z
Regular Article - Theoretical Physics
Realistic compactification in spatially flat vacuum cosmological models in cubic Lovelock gravity: high-dimensional case
Programa de Pós-Graduação em Física, Universidade Federal do Maranhão (UFMA), São Luís, Maranhão, 65085-580, Brazil
* e-mail: sergey.pavluchenko@gmail.com
Received:
5
July
2018
Accepted:
22
July
2018
Published online:
31
July
2018
In this paper we perform systematic investigation of all possible regimes in spatially flat vacuum cosmological models in cubic Lovelock gravity. The spatial section is considered as a product of three- and extra-dimensional isotropic subspaces, and the former represents our Universe. As the equations of motion are different for  and general
and general 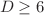 cases, we considered them all separately. This is the second paper of the series, and we consider
cases, we considered them all separately. This is the second paper of the series, and we consider  and general
and general 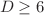 cases here. For each D case we found critical values for
cases here. For each D case we found critical values for  (Gauss–Bonnet coupling) and
(Gauss–Bonnet coupling) and  (cubic Lovelock coupling) which separate different dynamical cases, isotropic and anisotropic exponential solutions, and study the dynamics in each region to find all regimes for all initial conditions and for arbitrary values of
(cubic Lovelock coupling) which separate different dynamical cases, isotropic and anisotropic exponential solutions, and study the dynamics in each region to find all regimes for all initial conditions and for arbitrary values of  and
and  . The results suggest that in all
. The results suggest that in all  there are regimes with realistic compactification originating from so-called “generalized Taub” solution. The endpoint of the compactification regimes is either anisotropic exponential solution (for
there are regimes with realistic compactification originating from so-called “generalized Taub” solution. The endpoint of the compactification regimes is either anisotropic exponential solution (for  ,
, 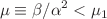 (including entire
(including entire 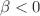 )) or standard Kasner regime (for
)) or standard Kasner regime (for  ,
, 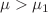 ). For
). For 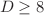 there is additional regime which originates from high-energy (cubic Lovelock) Kasner regime and ends as anisotropic exponential solution. It exists in two domains:
there is additional regime which originates from high-energy (cubic Lovelock) Kasner regime and ends as anisotropic exponential solution. It exists in two domains:  ,
, 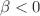 ,
,  and entire
and entire  ,
,  . Let us note that for
. Let us note that for 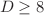 and
and  ,
, 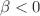 ,
, 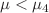 there are two realistic compactification regimes which exist at the same time and have two different anisotropic exponential solutions as a future asymptotes. For
there are two realistic compactification regimes which exist at the same time and have two different anisotropic exponential solutions as a future asymptotes. For 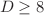 and
and  ,
,  ,
,  there are two realistic compactification regimes but they lead to the same anisotropic exponential solution. This behavior is quite different from the Einstein–Gauss–Bonnet case. There are two more unexpected observations among the results – all realistic compactification regimes exist only for
there are two realistic compactification regimes but they lead to the same anisotropic exponential solution. This behavior is quite different from the Einstein–Gauss–Bonnet case. There are two more unexpected observations among the results – all realistic compactification regimes exist only for  and there is no smooth transition from high-energy Kasner regime to the low-energy regime with realistic compactification.
and there is no smooth transition from high-energy Kasner regime to the low-energy regime with realistic compactification.
© The Author(s), 2018




