Neutrino propagation in an electron background with an inhomogeneous magnetic field

José F. Nieves; Sarira Sahu

doi:10.1140/epjc/s10052-018-6030-7

EPJ

a
b
c
d
e
ap
st
h
plus
ds
pv
ti
qt
am
n

2024 Impact factor 4.8

Particles and Fields

Open Access

Eur. Phys. J. C (2018) 78: 547
https://doi.org/10.1140/epjc/s10052-018-6030-7

Regular Article - Theoretical Physics

Neutrino propagation in an electron background with an inhomogeneous magnetic field

José F. Nieves¹ and Sarira Sahu²^,3^*

¹ Laboratory of Theoretical Physics, Department of Physics, University of Puerto Rico, Río Piedras, San Juan, 00936, Puerto Rico
² Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México, Circuito Exterior, C.U., A. Postal 70-543, 04510, Mexico DF, Mexico
³ Astrophysical Big Bang Laboratory, RIKEN, Hirosawa, Wako, Saitama, 351-0198, Japan

^* e-mail: sarira@nucleares.unam.mx

Received: 14 February 2018
Accepted: 23 June 2018
Published online: 4 July 2018

Abstract

We study the electromagnetic coupling of a neutrino that propagates in a two-stream electron background medium. Specifically, we calculate the electromagnetic vertex function for a medium that consists of a normal electron background plus another electron stream background that is moving with a velocity four-vector $v^\mu$ relative to the normal background. The results can be used as the basis for studying the neutrino electromagnetic properties and various processes in such a medium. As an application, we calculate the neutrino dispersion relation in the presence of an external magnetic field ( $\mathbf {B}$ ), focused in the case in which B is inhomogeneous, keeping only the terms of the lowest order in $$1/m^2_W$$ and linear in the B and its gradient. 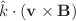We show that the dispersion relation contains additional anisotropic terms involving the derivatives of $\mathbf {B}$ , such as the gradient of ${\hat{k}}\cdot (\mathbf {v}\times \mathbf {B})$ , which involve the stream background velocity, and a term of the form ${\hat{k}}\cdot (\nabla \times \mathbf {B})$ that can be present in the absence of the stream background, in addition to a term of the form ${\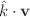hat{k}}\cdot \mathbf {v}$ and the well known term ${\hat{k}}\cdot \mathbf {B}$ that arises in the constant $\mathbf {B}$ case. The derivative-dependent terms are even under a CP transformation. As a result, in contrast to the latter two just mentioned, they depend on the sum of the particle and antiparticle densities and therefore can be non-zero in a CP-symmetric medium in which the particle and antiparticle densities are equal.