https://doi.org/10.1140/epjc/s10052-016-4060-6
Regular Article - Theoretical Physics
Thermodynamical aspects of running vacuum models
1
Departamento de Astronomia, Universidade de São Paulo, Rua do Matão 1226, 05508-900, São Paulo, Brazil
2
Academy of Athens, Research Center for Astronomy and Applied Mathematics, Soranou Efessiou 4, 11-527, Athens, Greece
3
High Energy Physics Group, Dept. d’Estructura i Constituents de la Matèria, Institut de Ciències del Cosmos (ICC), Univ. de Barcelona, Av. Diagonal 647, 08028, Barcelona, Catalonia, Spain
* e-mail: jas.lima@iag.usp.br
Received:
17
February
2016
Accepted:
1
April
2016
Published online:
25
April
2016
The thermal history of a large class of running vacuum models in which the effective cosmological term is described by a truncated power series of the Hubble rate, whose dominant term is 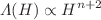 , is discussed in detail. Specifically, by assuming that the ultrarelativistic particles produced by the vacuum decay emerge into space-time in such a way that its energy density
, is discussed in detail. Specifically, by assuming that the ultrarelativistic particles produced by the vacuum decay emerge into space-time in such a way that its energy density 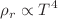 , the temperature evolution law and the increasing entropy function are analytically calculated. For the whole class of vacuum models explored here we find that the primeval value of the comoving radiation entropy density (associated to effectively massless particles) starts from zero and evolves extremely fast until reaching a maximum near the end of the vacuum decay phase, where it saturates. The late-time conservation of the radiation entropy during the adiabatic FRW phase also guarantees that the whole class of running vacuum models predicts the same correct value of the present day entropy,
, the temperature evolution law and the increasing entropy function are analytically calculated. For the whole class of vacuum models explored here we find that the primeval value of the comoving radiation entropy density (associated to effectively massless particles) starts from zero and evolves extremely fast until reaching a maximum near the end of the vacuum decay phase, where it saturates. The late-time conservation of the radiation entropy during the adiabatic FRW phase also guarantees that the whole class of running vacuum models predicts the same correct value of the present day entropy, 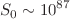 –
–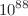 (in natural units), independently of the initial conditions. In addition, by assuming Gibbons–Hawking temperature as an initial condition, we find that the ratio between the late-time and primordial vacuum energy densities is in agreement with naive estimates from quantum field theory, namely,
(in natural units), independently of the initial conditions. In addition, by assuming Gibbons–Hawking temperature as an initial condition, we find that the ratio between the late-time and primordial vacuum energy densities is in agreement with naive estimates from quantum field theory, namely, 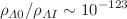 . Such results are independent on the power n and suggests that the observed Universe may evolve smoothly between two extreme, unstable, non-singular de Sitter phases.
. Such results are independent on the power n and suggests that the observed Universe may evolve smoothly between two extreme, unstable, non-singular de Sitter phases.
© The Author(s), 2016




