https://doi.org/10.1140/epjc/s10052-009-0866-9
Regular Article - Theoretical Physics
Non-hermitian quantum mechanics in non-commutative space
1
Theory Division, Saha Institute of Nuclear Physics, 1/AF Bidhannagar, Calcutta, 700064, India
2
Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata, 700108, India
* e-mail: pulakranjan.giri@saha.ac.in
Received:
13
August
2008
Revised:
4
November
2008
Published online:
5
February
2009
A recent investigation of the possibility of having a
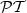-symmetric periodic potential in an optical lattice stimulated the urge to generalize non-hermitian quantum mechanics beyond the case of commutative space. We thus study non-hermitian quantum systems in non-commutative space as well as a
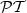-symmetric deformation of this space. Specifically, a
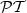-symmetric harmonic oscillator together with an iC(x
1+x
2) interaction are discussed in this space, and solutions are obtained. We show that in the
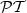deformed non-commutative space the Hamiltonian may or may not possess real eigenvalues, depending on the choice of the non-commutative parameters. However, it is shown that in standard non-commutative space, the iC(x
1+x
2) interaction generates only real eigenvalues despite the fact that the Hamiltonian is not
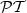-symmetric. A complex interacting anisotropic oscillator system also is discussed.
PACS: 03.65.-w – / 03.65.Db – / 03.65.Ta –
© Springer-Verlag, 2009
