T-dependent Dyson-Schwinger equation in IR regime of QCD: the critical point

A. N. Mitra; W-Y. P. Hwang

doi:10.1140/epjc/s2004-02072-3

EPJ

T-dependent Dyson-Schwinger equation in IR regime of QCD: the critical point

A. N. Mitra^* and W-Y. P. Hwang

Center for Academic Excellence on Cosmology & Particle Astrophysics, National Taiwan University, Taipei 106, Taiwan, R.O.C

Abstract

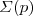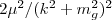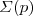The quark mass function $\Sigma(p)$ in QCD is revisited, using a gluon propagator in the form 1/(k ² + m _g ²) plus $2\mu^2/ (k^2 + m_g^2)^2$ , where the second (IR) term gives linear confinement for m _g = 0 in the instantaneous limit, μ being another scale. To find $\Sigma(p)$ we propose a new (differential) form of the Dyson-Schwinger equation (DSE) for 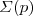$\Sigma(p)$ , based on an infinitesimal subtractive renormalization via a differential operator which lowers the degree of divergence in integration on the RHS, by two units. 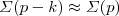This warrants $\Sigma(p-k)\approx \Sigma(p)$ in the integrand since its k-dependence is no longer sensitive to the principal term (p-k)² in the quark propagator. 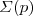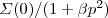The simplified DSE (which incorporates the Ward-Takahashi (WT) identity in the Landau gauge) is satisfied for large p ² by $\Sigma(p)$ = $\Sigma(0)/(1 + \beta p^2)$ , except for Log factors. 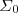The limit p ² = 0 determines $\Sigma_0$ . 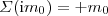A third limit, p ² = -m ₀ ², defines the dynamical mass m ₀ via $\Sigma({\mathrm {i}} m_0) = + m_0$ . 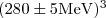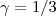After two checks ( $f_{\pi} = 93\pm 1$ MeV and $\langle q{\bar{q}}\rangle$ = $(280 \pm 5 {\mathrm {MeV}})^3$ ), for $1.5 < \beta < 2$ with $\Sigma_0 = 300$ MeV, the T-dependent DSE is used in the real time formalism to determine the “critical” index $\gamma = 1/3$ analytically, with the IR term partly serving as the H-field. We find 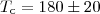$T_{\mathrm {c}} = 180 \pm 20$ MeV and check the vanishing of $f_{\pi}$ and $\langle q{\bar{q}}\rangle$ at T _c.

15th European Conference on Atoms Molecules and Photons (ECAMP)
June 30 to July 4, 2025
Innsbruck, Austria

EPJ

T-dependent Dyson-Schwinger equation in IR regime of QCD: the critical point

Conference announcements