EPJ

2024 Impact factor 4.8
EPJ C - Particles and Fields
Particles and Fields
Eur. Phys. J. C 4, 259-263
DOI 10.1007/s100529800772

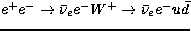
Gauge invariance in the process $e^+e^-\rightarrow \bar \nu_e e^-W^+ \rightarrow\bar\nu_e e^-u\bar d$

Robin G. Stuart

Randall Laboratory of Physics, University of Michigan, Ann Arbor, MI 48109-1120, USA

Received: 1 March 1997 / Revised version: 19 September 1997 / Published online: 26 February 1998

Abstract
The process $e^+e^-\rightarrow \bar \nu_e e^-W^+ \rightarrow\bar\nu_e e^-u\bar d$ is considered as an example of the problems associated with maintaining gauge invariance in matrix elements involving unstable particles. It is shown how to construct a matrix element that correctly treats width effects for the intermediate unstable W boson and that is both SU(2)L and $U(1)_{\rm e.m.}$ gauge-invariant. SU(2)L gauge-invariance is maintained by Laurent expansion in kinematic invariants and $U(1)_{\rm e.m.}$gauge-invariance is enforced by means of projection operator under which the exact matrix element is invariant.

Copyright Springer-Verlag

Conference announcements