DOI 10.1007/s100529800706
Four loop anomalous dimensions of gradient operators
in
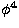theory
S.É. Derkachov1 - J.A. Gracey2 - A.N. Manashov3
1 Department of Mathematics, St Petersburg Technology
Institute, Sankt Petersburg, Russia (e-mail:
derk@tu.spb.ru)
2 Theoretical Physics Division, Department of Mathematical Sciences,
University of Liverpool, Liverpool, L69 7ZF,
United Kingdom (e-mail:
jag@amtp.liv.ac.uk)
3 Department of Theoretical Physics, State University of St
Petersburg, Sankt Petersburg, 198904 Russia
(e-mail:
manashov@snoopy.phys.spbu.ru)
Received: 12 May 1997 / Published online: 20 February 1998
Abstract
We compute the anomalous dimensions of a set of composite operators which
involve derivatives at four loops in 
in 
theory as a function
of the operator moment n. These operators are similar to the twist-2
operators which arise in QCD in the operator product expansion in deep
inelastic scattering. By regarding their inverse Mellin transform as being
equivalent to the DGLAP splitting functions we explore to what extent taking a
restricted set of operator moments can give a good approximation to the
exact four loop result.
Copyright Springer-Verlag
