https://doi.org/10.1140/epjc/s10052-025-13816-8
Regular Article - Theoretical Physics
Nonextensive black hole thermodynamics from generalized Euclidean path integral and Wick’s rotation
1
LPTHE, Physics Department, Faculty of Sciences, Ibnou Zohr University, Agadir, Morocco
2
CRMEF, Regional Center for Education and Training Professions, Marrakesh, Morocco
3
Laboratory of High Energy Physics and Condensed Matter HASSAN II University, Faculty of Sciences Ain Chock, Casablanca, Morocco
Received:
9
November
2024
Accepted:
14
January
2025
Published online:
24
January
2025
This paper extends the Euclidean path integral formalism to account for nonextensive thermodynamics. Concretely, we introduce a generalized Wick’s rotation from real time t to imaginary time  such that,
such that, 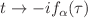 , where
, where 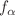 a differentiable function and
a differentiable function and 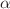 is a parameter related to nonextensivity. The standard extensive formalism is recovered in the limit
is a parameter related to nonextensivity. The standard extensive formalism is recovered in the limit 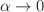 and
and 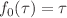 . Furthermore, we apply this generalized Euclidean path integral to black hole thermodynamics and derive the generalized Wick’s rotations given the nonextensive statistics. The proposed formulation enables the treatment of nonextensive statistics on the same footing as extensive Boltzmann–Gibbs statistics. Moreover, we define a universal measure,
. Furthermore, we apply this generalized Euclidean path integral to black hole thermodynamics and derive the generalized Wick’s rotations given the nonextensive statistics. The proposed formulation enables the treatment of nonextensive statistics on the same footing as extensive Boltzmann–Gibbs statistics. Moreover, we define a universal measure, 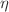 , for the nonextensivity character of statistics. Lastly, based on the present formalism, we strengthen the equivalence between the AdS-Schwarzschild black hole in Boltzmann–Gibbs statistics and the flat-Schwarzschild black hole within Rényi statistics and suggest a potential reformulation of the
, for the nonextensivity character of statistics. Lastly, based on the present formalism, we strengthen the equivalence between the AdS-Schwarzschild black hole in Boltzmann–Gibbs statistics and the flat-Schwarzschild black hole within Rényi statistics and suggest a potential reformulation of the 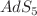 /
/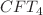 duality.
duality.
In this article, the affiliation details for the second and third affiliations were interchanged.
An erratum to this article is available online at https://doi.org/10.1140/epjc/s10052-025-13904-9.
© The Author(s) 2025
corrected publication 2025
 Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.




